При оценке безопасности ассиметричных криптографических протоколов, обычно предполагается, что противник имеет полное описание протокола и алгоритмов в него входящих, владеет публичными ключами, а секретным является только закрытый ключ. Кроме того, противник может перехватить некоторые данные, которыми обмениваются легитимные участники, и может даже осуществлять некоторый контроль над природой этих данных (например, путем выбора сообщений для подписи, если целью является  компрометация секретного ключа, используемого при создании цифровой подписи) [1]. Как правило, криптографические протоколы остаются полностью устойчивыми с математической точки зрения, даже с учетом всех указанных допущений.

В последнее время для осуществления атак на криптографические протоколы и алгоритмы все чаще используются так называемые побочные каналы (side-channel attacks). Утечка информации через такие каналы чаще всего не предусматривается в классической модели безопасности протокола.

В данном докладе продемонстрирована возможность проведения атаки на аппаратное устройство, реализующее алгоритм ECDSA - стандарт создания электронной цифровой подписи базирующийся на арифметике эллиптических кривых.

Как правило, для создания аппаратной реализации устройств шифрования и выработки ЭЦП используются логические элементы на базе КМОП (CMOS) технологии. Основываясь на физических принципах работы КМОП микросхем и получив доступ к ненадежному источнику питания, используемому аппаратным устройством для осуществления генерации ЭЦП, можно провести анализ потребляемой им мощности.

В алгоритмах, базирующихся на эллиптических кривых (в том числе и в рассматриваемом ECDSA алгоритме) используются два типа операций - сложение чисел на эллиптической кривой и удвоение числа. Допуская, что устройство, выполняющее вычислительные операции при создании электронной цифровой подписи по стандарту ECDSA, подключено к незащищенному источнику питания, к которому имеет доступ злоумышленник, недоброжелатель может получить осциллограмму потребления мощности данным устройством.

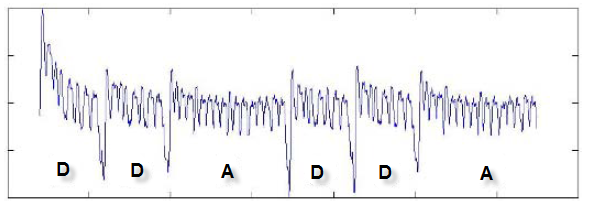
Рис. 1 Потребление мощности устройством при проведении операции сложения (A) и удвоения (D) на эллиптической кривой над простым полем.

На графике потребления мощности аппаратным устройством (рис.1) можно четко выделить проведение данных операций в пределах одного вычислительного такта. На приведенной осциллограмме участки D (double) соответствуют операции удваивания числа на эллиптической кривой, а участки A (addition) - операции сложения двух чисел на эллиптической кривой.

Допуская, что модуль эллиптической кривой известен, известно подписываемое сообщение, и в пределах одного сообщения используется один и тот же секретный ключ, основываясь на полученных с осциллограммы данных и используя известный алгоритм [2], можно восстановить используемый закрытый ключ.

Существует несколько методов противодействия такого рода атакам, но, как правило, контрмеры включают в себя предумышленные изменения в алгоритмах – внедрение дополнительных «пустых» операций.

Эффективность контрмер в значительной степени зависит от характеристик аппаратной платформы, операционной среды, возможностей противника и должна оцениваться на основе каждого конкретного случая.

В качестве примера на рис.2 показан, результат маскировки последовательности операций сложения и удваивания на эллиптической кривой над простым полем. Операции-«пустышки» были включены в алгоритмы для сложения и удвоения таким образом, что последовательность элементарных операций выполняемых при удваивании, ровно два раза используются в операции сложения, тем самым маскируя операцию сложения.

Рис. 2 Маскировка операции сложения на эллиптической кривой путем введения «пустых» операций.

Таким образом, авторами заостряется внимание на необходимости учета возможности утечки информации по побочным каналам и предлагаются способы борьбы с такого-рода уязвимостями.

Литература

1. Болотов А.А. «Элементарное введение в эллиптическую криптографию. Алгебраические и алгоритмические основы» - М, 2006.

2. D. Hankerson, A. Menezes. «Guide to Elliptic Curve Cryptography» - Springer, 2009.

АРТАМОНОВ В.А., КОРОТКЕВИЧ О.С.

г.Минск, Белорусский Национальный Технический Университет

Отправить статью в социальные сети, на печать, e-mail и в другие сервисы: